Linear Regression-Theory
Linear regression is a supervised machine learning technique where we need to predict a continuous output, which has a constant slope.
There are two main types of linear regression:
1. Simple Regression:
Through simple linear regression we predict response using single features.
If you recall, the line equation (y = mx + c) we studied in schools. Let’s understand what these parameters say and how this equation works in linear regression.
Y = βo + β1X + ∈
Where, Y = Dependent Variable ( This is the variable which we want to predict )
X = Independent Variable ( This is the variable which we use to make prediction )
βo – This is the intercept term. It is the prediction value you get when X = 0
β1 – This is the slope term. It explains the change in Y when X changes by 1 unit.
∈ – This represents the residual value, i.e. the difference between actual and predicted values.
2. Multivariable regression:
It is nothing but extension of simple linear regression. It attempts to model the relationship between two or more features and a response by fitting a linear equation to observed data.
Multi variable linear equation might look like this, where w represents the coefficients, or weights, our model will try to learn.
f(x,y,z)=w1x+w2y+w3z
Let’s understand it with example.
In a company for sales predictions, these attributes might include a company’s advertising spend on radio, TV, and newspapers.
Sales=w1Radio+w2TV+w3News
Linear Regression geometrical representation
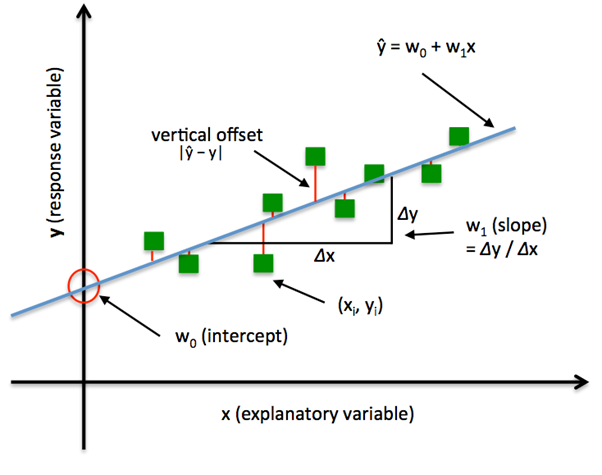
So our goal in linear regression model is:
Find a line or plane that best fits the data points. Here best fit means minimise the sum of errors across our training data.
Types of Deliverable in linear regression:
Typically there are following questions that a business wanted to know
- They wanted to know their sales or profit prediction.
- Drivers(What drives the sales?)
- All variable that have significant beta.
- Which factors are detrimental /incremental?
- All the drivers, which one should target first?(Variable with highest absolute value)
- How to predict drivers?
- To answer this question, you need calculate (beta*X )for each X variable and you need to choose the highest value and accordingly you can choose your driver after that convince business why you have chosen the particular driver.
So now the question arises how we calculate Beta values?
To calculate the beta values we will use OLS(ordinary least squared) method.
Assumptions of Linear Regression:
1. X variables (Explanatory variable) should be linearly related to Y (Response Variable):
Meaning:
If you plot a scatter plot between x variable and Y, most of the data point should be around the straight line.
How to check?
Draw the scatter plot between each x variable and y variable.
What happens if the assumption is violated?
MSE(Mean Squared Error) will be high. MSE is nothing but the average of squared error occurred between the predicted values and actual values. It can be written as:
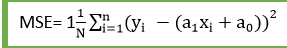
Where,
N=Total number of observation
Yi = Actual value
(a1xi+a0)= Predicted value.
What to do if variable is not linear?
- Drop the variable – But in this case will loose the information.
- Take log(x+1) of x variables.
2.Residual or the Y variable should be normally distributed:
Meaning:
Residuals (errors) or Y, when plotted in a histogram produces a bell shaped curve.
Residuals: The distance between the actual value and predicted values is called residual. If the observed points are far from the regression line, then the residual will be high, and so cost function will high. If the scatter points are close to the regression line, then the residual will be small and hence the cost function.
How to check?
Plot a histogram of Y, when plotted histogram produces a bell- shaped curve then it follows normality.
Or we can also use q-q plot(quantile- quantile plot) of residuals
What happens if the assumption is violated?
It means all the P values has been calculated wrongly.
What to do if assumption is violated?
In that case we need to transform our Y such a way so that it become normal. To do that we need to use log of Y.
3.There should not be any relationship between X variables (i.e no multicollinearity)
Meaning:
X variable should not have any linear relationship between themselves. It’s obvious that we don’t want same information in repeat mode.
How to check?
- Calculate correlation between every X with every other X variable.
- Second method is to, calculate VIF(Variance influence factor)
What happens if the assumption is violated?
Your beta’s values sign will fluctuate.
What to do if assumption is violated?
Drop those X variable whose VIF is greater than 10(VIF>10)
4. The variance of error should remain constant over value of Y (Homoscedasticity/ No heteroskedasticity )
Meaning:
Spread of residuals should remain constant with values of Y.
How to check?
Draw scatter plot of residuals VS Y.
What happens if the assumption is violated?
Your P value will not accurate.
What to do if assumption is violated?
In that case we need to transform our Y such a way so that it become normal. To do that we need to use log of Y.
5. There should not be any auto-correlation between the residuals.
Meaning:
Correlation of residuals with lead residuals. Here lead residuals means next calculated residual.
How to check?
Use DW stats(Durbin Watson Stats)
If DW stats ~ 2, then no auto correlation.
What happens if the assumption is violated?
Your P value will not accurate.
What to do if assumption is violated?
Understand the reason why it is happening?
If autocorrelation is due to Y then cannot build linear regression model.
If autocorrelation is due to X then drop that X variable.
How to check Model Performance?
The Goodness of fit determines how the line of regression fits the set of observations. The process of finding the best model out of various models is called optimization. It can be achieved by below method:
R-squared method:
- R-squared is a statistical method that determines the goodness of fit.
- It measures the strength of the relationship between the dependent and independent variables on a scale of 0-100%.
- The high value of R-square determines the less difference between the predicted values and actual values and hence represents a good model.
- It is also called a coefficient of determination, or coefficient of multiple determination for multiple regression.
- It can be calculated from the below formula:
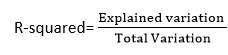
In the next lecture we will see how to implement leaner regression in python.
1 comment so far