Decision Tree – Theory
Decision tree is very simple yet a powerful algorithm for classification and regression. As name suggest it has tree like structure. It is a non-parametric technique. A decision tree typically starts with a single node, which branches into possible outcomes. Each of those outcomes leads to additional nodes, which branch off into other possibilities. This gives it a treelike shape.
For example of a decision tree can be explained using below binary tree. Let’s suppose you want to predict whether a person is fit by their given information like age, eating habit, and physical activity, etc. The decision nodes here are questions like ‘What’s the age?’, ‘Does he exercise?’, ‘Does he eat a lot of pizzas’? And the leaves, which are outcomes like either ‘fit’, or ‘unfit’. In this case this was a binary classification problem (yes or no type problem).
There are two main types of Decision Trees:
Classification trees (Yes/No types)
What we’ve seen above is an example of classification tree, where the outcome was a variable like ‘fit’ or ‘unfit’. Here the decision variable is categorical.
Regression trees (Continuous data types)
Here the decision or the outcome variable is Continuous, e.g. a number like 123.
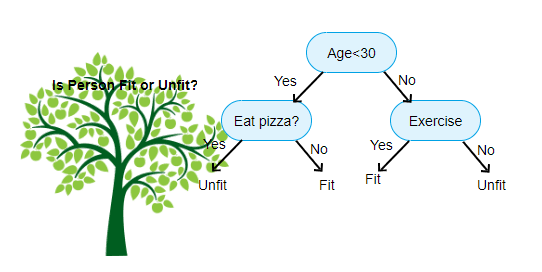
The top-most item, in this example, “Age < 30 ?” is called the root. It’s where everything starts from. Branches are what we call each line. A leaf is everything that isn’t the root or a branch.
A general algorithm for a decision tree can be described as follows:
- Pick the best attribute/feature. The best attribute is one which best splits or separates the data.
- Ask the relevant question.
- Follow the answer path.
- Go to step 1 until you arrive to the answer.
Terms used with Decision Trees:
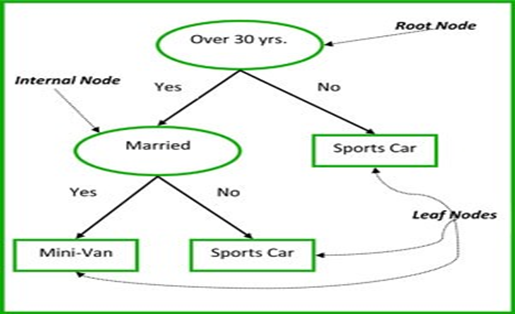
- Root Node – It represents entire population or sample and this further gets divided into two or more similar sets.
- Splitting – Process to divide a node into two or more sub nodes.
- Decision Node – A sub node is divided further sub node, called decision node.
- Leaf/Terminal Node – Node which do not split further called leaf node.
- Pruning – When we remove sub-nodes of a decision node, this process is called pruning.
- Branch/ Sub-tree – A sub-section of entire tree is called branch or subtree.
- Parent and child node – A node, which is divided into sub-nodes is called parent node of sub-nodes whereas sub-nodes are the child of parent node.
Let’s understand above terms with the below image
Types of Decision Trees
- Categorical Variable decision tree – Decision Tree which has categorical target variable then it called as categorical variable.
- Continuous Variable Decision Tree – Decision Tree which has continuous target variable then it is called as Continuous Variable Decision Tree.
Advantages of Decision Tree
- Easy to understand – Algorithm is very easy to understand even for people from non-analytical background. A person without statistical knowledge can interpret them.
- Useful in data exploration – It is the fastest algorithm to identify most significant variables and relation between variables. It help us to identify those variables which has better power to predict target variable.
- Decision tree do not required more effort from user side for data preparation.
- This algorithm is not affected by outliers or missing value to an extent, so it required less data cleaning effort as compare to other model.
- This model can handle both numerical and categorical variables.
- The number of hyper-parameters to be tuned is almost null.
Disadvantages of Decision Tree
- Over Fitting – It is the most common problem in decision tree. This issue has resolved by setting constraints on model parameters and pruning. Over fitting is an phenomena where your model create a complex tree that do not generalize the data very well.
- Small variations in the data can result completely different tree which mean it unstable the model. This problem is called variance, which need to lower by method like bagging and boosting.
- If some class is dominate in your model then decision tree learner can create a biased tree. So it is recommended to balance the data set prior to fitting with the decision tree.
- Calculations can become complex when there are many class label.
Decision Tree Flowchart
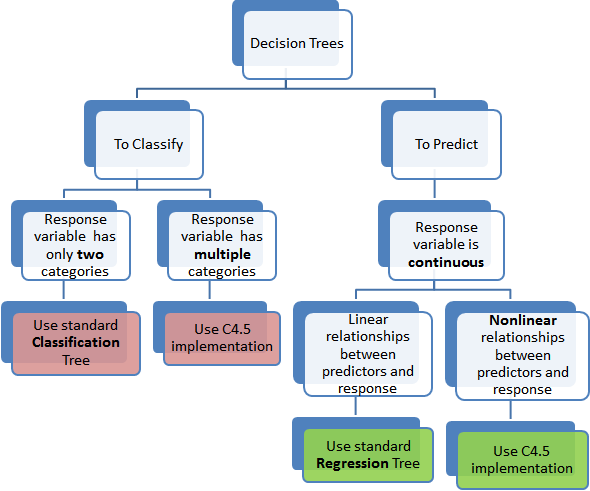
How does a tree decide where to split?
In decision tree making splits effect the accuracy of model. The decision criteria are different for classification and regression trees. Decision tree splits the nodes on all available variables and then selects the split which results in most homogeneous sub-nodes.
The algorithm selection is also based on type of target variables. The four most commonly used algorithms in decision tree are:
- CHAID – Chi-Square Interaction Detector
- CART – Classification and regression trees.
Let’s discuss both methods in detail
CHAID – Chi-Square Interaction Detector
It is an algorithm to find out the statistical significance between the differences between sub-nodes and parent node. It works with categorical target variable such as “yes” or “no”.
Algorithm follows following steps:
- Iterate all available x variables.
- Check if the variable is numeric
- If the variable is numeric make it categorical by decile and percentile.
- Figure out all possible cuts.
- For each possible cut it will do Chi-Square test and store the P value
- Choose that cut which give least p value.
- Cut the data using that variable and that cut which gives least P value.
CART – Classification and regression trees
There are basically two subtypes for this algorithm.
Gini index:
It says, if we select two items from a population at random then they must be of same class and probability for this is 1 if population is pure. It works with categorical target variable “Success” or “Failure”.
Gini = 1-P^2 – (1-p)^2 , Here p is the probability
Gain = Gini of parents leaf – weighted average of Gini of the nodes (Weights are proportional to population of each child node)
Steps to Calculate Gini for a split
- Iterate all available x variables.
- Check if the variable is numeric
- If the variable is numeric make it categorical by decile and percentile.
- Figure out all possible cuts.
- Calculate gain for each split
- Choose that cut which gives the highest cut.
- Cut the data using that variable and that cut which gives maximum gain
Entropy Tree:
To understand entropy tree we need to first understand what entropy is?
Entropy – Entropy is basically measures the level of impurity in a group of examples. If the sample is completely homogeneous, then the entropy is zero and if the sample is an equally divided (50% — 50%), it has entropy of one.
Entropy = -p log2 p — q log2q
Here p and q is the probability of success and failure respectively in that node. Entropy is also used with categorical target variable. It chooses the split which has lowest entropy compared to parent node and other splits. The lesser the entropy, the better it is.
Gain = Entropy of parents leaf – weighted average of entropy of the nodes (Weights are proportional to population of each child node)
Steps to Calculate Entropy for a split
- Iterate all available x variables.
- Check if the variable is numeric
- If the variable is numeric make it categorical by decile and percentile.
- Figure out all possible cuts.
- Calculate gain for each split
- Choose that cut which gives the highest cut.
- Cut the data using that variable and that cut which gives maximum gain.
Decision Tree Regression
As we have discussed above with the help of decision tree we can also solve the regression problem. So let’s see what the steps are.
Following steps are involved in algorithm.
- Iterate all available x variables.
- Check if the variable is numeric
- If the variable is numeric make it categorical by decile and percentile.
- Figure out all possible cuts.
- For each cuts calculate MSE
- Choose that cut and that variable which gives the minimum MSE.
- Cut the data using that variable and that cut which gives minimum MSE.
Stopping Criteria of Decision Tree
- Pure Node – If tree find a pure node, that particular leaf will stop growing.
- User defined depth
- Minimum observation in the node
- Minimum observation in the leaf